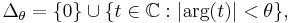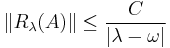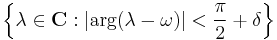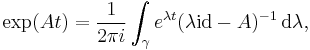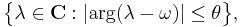Analytic semigroup

In mathematics, an analytic semigroup is particular kind of strongly continuous semigroup. Analytic semigroups are used in the solution of partial differential equations; compared to strongly continuous semigroups, analytic semigroups provide better regularity of solutions to initial value problems, better results concerning perturbations of the infinitesimal generator, and a relationship between the type of the semigroup and the spectrum of the infinitesimal generator.

Definition

Let Γ(t) = exp(At) be a strongly continuous one-parameter semigroup on a Banach space (X, ||·||) with infinitesimal generator A. Γ is said to be an analytic semigroup if

for some 0 < θ < π ⁄ 2, the continuous linear operator exp(At) : X → X can be extended to t ∈ Δ_θ,

$\Delta_{\theta} = \{ 0 \} \cup \{ t \in \mathbb{C}�: | \mathrm{arg}(t) | < \theta \},$

and the usual semigroup conditions hold for s, t ∈ Δ_θ: exp(A0) = id, exp(A(t + s)) = exp(At)exp(As), and, for each x ∈ X, exp(At)x is continuous in t;

and, for all t ∈ Δ_θ \ {0}, exp(At) is analytic in t in the sense of the uniform operator topology.

Characterization

The infinitesimal generators of analytic semigroups have the following characterization:

A closed, densely-defined linear operator A on a Banach space X is the generator of an analytic semigroup if and only if there exists an ω ∈ R such that the half-plane Re(λ) > ω is contained in the resolvent set of A and, moreover, there is a constant C such that

$\| R_{\lambda} (A) \| \leq \frac{C}{| \lambda - \omega |}$

for Re(λ) > ω. If this is the case, then the resolvent set actually contains a sector of the form

$\left\{ \lambda \in \mathbf{C}�: | \mathrm{arg} (\lambda - \omega) | < \frac{\pi}{2} %2B \delta \right\}$

for some δ > 0, and an analogous resolvent estimate holds in this sector. Moreover, the semigroup is represented by

$\exp (At) = \frac1{2 \pi i} \int_{\gamma} e^{\lambda t} ( \lambda \mathrm{id} - A )^{-1} \, \mathrm{d} \lambda,$

where γ is any curve from e^−iθ∞ to e^+iθ∞ such that γ lies entirely in the sector

$\big\{ \lambda \in \mathbf{C}�: | \mathrm{arg} (\lambda - \omega) | \leq \theta \big\},$

with π ⁄ 2 < θ < π ⁄ 2 + δ.

References

Renardy, Michael; Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second edition ed.). New York: Springer-Verlag. pp. xiv+434. ISBN 0-387-00444-0. MR 2028503.